Giá trị tương lai của dòng tiền có vai trò quan trọng trong việc đầu tư cá nhân hay tổ chức doanh nghiệp. Vậy nó được ứng dụng ra sao? Cách tính như thế nào? Mời các bạn cùng tham khảo bài viết dưới đây.

Giá trị tương lai của dòng tiền là gì?
Giá trị tương lai của tiền trong tiếng Anh là Future Value of Money, viết tắt là FV. Giá trị tương lai của tiền được hiểu là giá trị tương tai của một khoản tiền hoặc dòng tiền ở thời điểm hiện tại.
Trong đó:
- Giá trị tương lai của một khoản tiền là giá trị có thể nhận được tại một thời điểm trong tương lai. Bao gồm số vốn gốc và toàn bộ số tiền lãi tính đến thời điểm đó.
- Giá trị tương lai của dòng tiền được xác định bằng tổng giá trị tương lai của tất cả các khoản tiền trong dòng tiền tệ đó.

Việc sử dụng công thức giá trị tương lai là rất lớn, giúp chúng ta có nhiều thông tin và có tầm nhìn xa hơn:
- Cách sử dụng tốt nhất của công thức giá trị tương lai là để tìm ra giá trị của các khoản đầu tư sẽ có giá trị sau một khoảng thời gian.
- Công ty Tài chính Doanh nghiệp sử dụng công thức Giá trị tương lai để đưa ra các quyết định hiệu quả trong việc định giá chi phí vốn.
- Bạn có thể tính số lần trả góp trên số tiền vay
- Bạn có thể tính toán số tiền tiết kiệm cần thiết để đạt được mục tiêu tài chính khi lợi nhuận gộp trong nhiều năm có hiệu quả với bạn.
- Tính toán niên kim, thu nhập của các khoản đầu tư theo thời gian.
Có thể bạn quan tâm: Dòng tiền tự do
Công thức tính

Công thức tổng quát
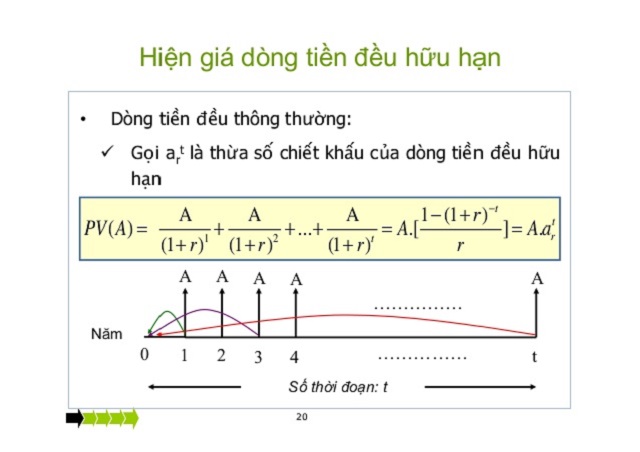
Công thức chung cho giá trị tương lai của tiền:
FV = PV(1+r)^n
Trong công thức này:
- FV: Giá trị tương lai của số tiền hiện tại
- PV: Giá trị hiện tại hoặc số tiền bạn có
- r: tỷ suất sinh lợi
- n: năm/kỳ
Việc xác định FV của một tài sản có thể phức tạp, tùy thuộc vào loại tài sản. Cần lưu ý rằng công thức tính FV dựa trên giả định về tốc độ tăng trưởng ổn định. Nếu tiền được gửi vào tài khoản tiết kiệm với lãi suất đảm bảo thì giá trị tương lai rất dễ xác định chính xác.
Tuy nhiên, đầu tư vào thị trường chứng khoán hoặc các loại chứng khoán khác có lợi nhuận biến động nhiều hơn có thể gặp khó khăn lớn hơn.
Hãy xem thêm: Đầu tư trái phiếu Techcombank
Ví dụ minh họa
Tính giá trị tương lai của 15.000.000 đồng được cho vay với lãi suất 12% mỗi năm trong 10 năm.
Ta có:
- PV = 15.000.000
- R = 12%
- N = 10
Khi đó: FV = PV (1 + R) n = 15.000.000 (1 + 0,12) 10 = 46.587.720
Vậy giá trị tương lai của 15.000.000 đồng sau 10 năm với lãi suất là 12% là 46.587.720 đồng.
Công thức cụ thể theo từng trường hợp
Trường hợp 1: Giá trị tương lai của dòng tiền cuối kỳ

- Nếu các khoản tiền phát sinh ở cuối mỗi kỳ không bằng nhau:
- Nếu các khoản tiền phát sinh ở cuối mỗi kỳ bằng nhau:
Khi các khoản tiền phát sinh ở cuối các thời điểm bằng nhau CF1 = CF2 = … CFn = A thì giá trị tương lai của dòng tiền đều cuối kỳ được xác định như sau:
Trường hợp 2: Giá trị tương lai của dòng tiền đầu kỳ

- Nếu các khoản tiền phát sinh ở đầu mỗi kỳ không bằng nhau:
- Nếu các khoản tiền phát sinh ở đầu mỗi kỳ bằng nhau:
Nếu các khoản tiền phát sinh ở đầu mỗi kỳ bằng nhau (CF1 = CF2 = … CFn = A)
Ví dụ minh họa

Doanh nghiệp TCBS có nghĩa vụ phải thanh toán một khoản tiền 101.304.000 đồng vào thời điểm sau 5 năm. TCBS muốn lập quỹ trả nợ bằng cách hàng năm gửi đều đặn số tiền vào ngân hàng với lãi suất tiền gửi 8%/năm (theo phương pháp tính lãi kép). Vậy TCBS phải gửi vào ngân hàng mỗi năm bao nhiêu tiền để cuối năm thứ 5 có đủ tiền trả nợ?
Giả sử số tiền gửi đều đặn hàng năm bằng A, trong 5 năm (bắt đầu từ thời điểm ngày hôm nay).
Có thể bạn quan tâm: Cách tính tiền lãi ngân hàng
Ứng dụng giá trị theo thời gian của dòng tiền

Xác định lãi suất
Trong trường hợp đã biết giá trị tương lai, giá trị vốn gốc và kỳ hạn tính lãi hoặc đã biết giá trị hiện tại, giá trị các khoản tiền phát sinh trong tương lai và kỳ tính lãi thì dựa vào công thức thích hợp tính giá trị tương lai hoặc tính giá trị hiện tại của tiền đó để xác định yếu tố lãi suất.
Xác định kỳ hạn
Trong trường hợp đã biết giá trị tương lai, giá trị vốn gốc và lãi suất hoặc đã biết giá trị hiện tại, giá trị các khoản tiền phát sinh trong tương lai và lãi suất thì dựa vào công thức thích hợp tính giá trị tương lai hoặc tính giá trị hiện tại của tiền đó từ đó xác định được yếu tố kỳ hạn.
Xác định khoản tiền phải thanh toán
Trường hợp này trong hợp đồng tín dụng trả dần đều mua hàng trả góp.

Ứng dụng khác
Ngoài một số ứng dụng đã nêu trên, lý thuyết giá trị theo thời gian của tiền được vận dụng rộng rãi trong các nghiệp vụ tài chính của doanh nghiệp cũng như các hoạt động đầu tư của doanh nghiệp. Đồng thời của các nhà đầu tư cá nhân, như vận dụng trong việc đánh giá hiệu quả đầu tư, ước định giá chứng khoán…
Như vậy, tính toán giá trị tương lai dòng tiền là cực kỳ cần thiết và đóng vai trò quan trọng trong việc đầu tư một cá nhân hay doanh nghiệp. Trên đây là bài viết thể hiện một số điểm cơ bản về giá trị tương lai của dòng tiền . Hy vọng sẽ giúp các bạn có thêm kiến thức bổ ích. Chúc các nhà đầu tư luôn thành công!
Bài viết tham khảo: